🚶‍♂️ Queues

The Features of Queue

Queue is a list or collection with the restriction that insertion can be performed at one end(rear) and deletion can be performed at other end(head). —First In First Out(FIFO)

Operation:

1. EnQueue(x) or Push(x);
2. DeQueue() or Pop();
3. Front() or Peek();
4. IsEmpty()
5. IsFull()

The operation above should be performed in the constant time. Their time complexity should be O(1).

The logistic view of Queue is showed as follow:

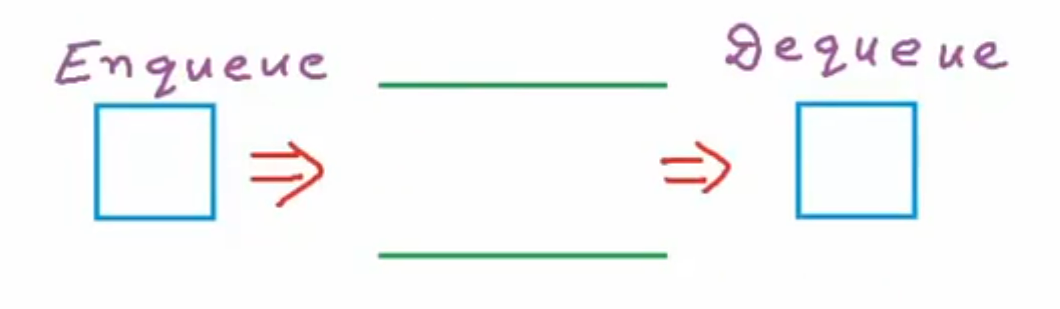
Applications

• Printer queue
• Process scheduling
• Simulating wait

Array Implementation

This the logistic view of array implementation. We set the length of queue by controlling the front and the rear.

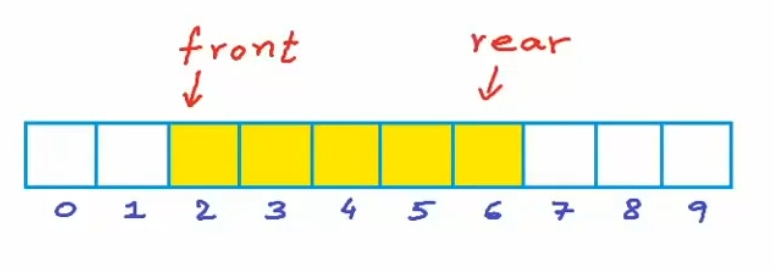
When the end of queue arrived the end of the memory block, the DeQueue operation makes the other space unused, and the EnQueue operation is invalid, seen as figure below. So circular array was supposed to solve this problem. It builds the array loop, so that the final index elements can be moved to the first index.

The first two cells are not available. They are wasted!

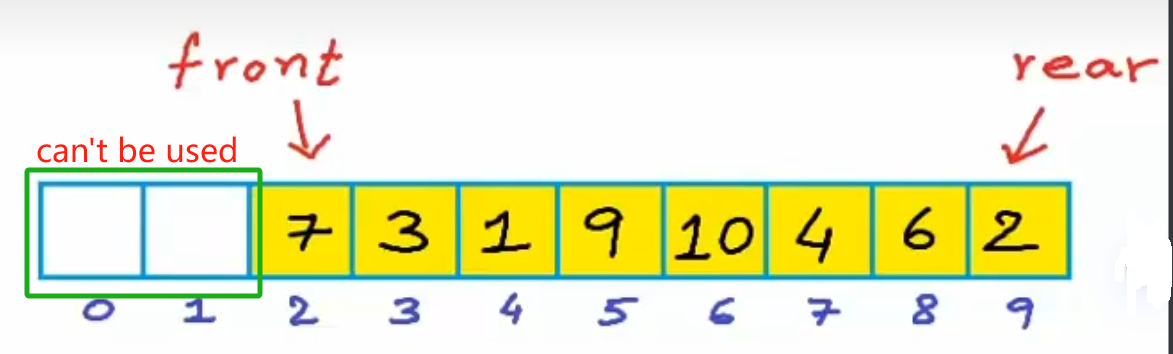
The first two cells are not available. They are wasted!

First, let’s see how to implement a queue through linear arrays.

// for the linear array, the queue can be implemented as follow. (qseudocode)
LinearArrayImplementation(){
	int A[10];
	front <- -1;
	rear <- -1;
	// for an empty queue, the front and the rear are both equal to -1.
}
IsEmpty(){
	if front==-1 && rear == -1
	return true
	else
	return false
}
IsFull(){
	if rear == size(A) - 1
	return true
	else
	return false
}
Enqueue(){
	if IsFull()
		print "queue is full"
		return
	else if IsEmpty()
		front<-rear<0
	else
		rear<-rear+1

	A[rear] <- x
}
Dequeue(){
	if IsEmpty()
		return
	else if front==rear
		front <- rear <- -1
	else
		front <- front + 1
}

Then, the circular array method can be achieved as pseudocode below. But there is something deserving attention.

The circular array diagram

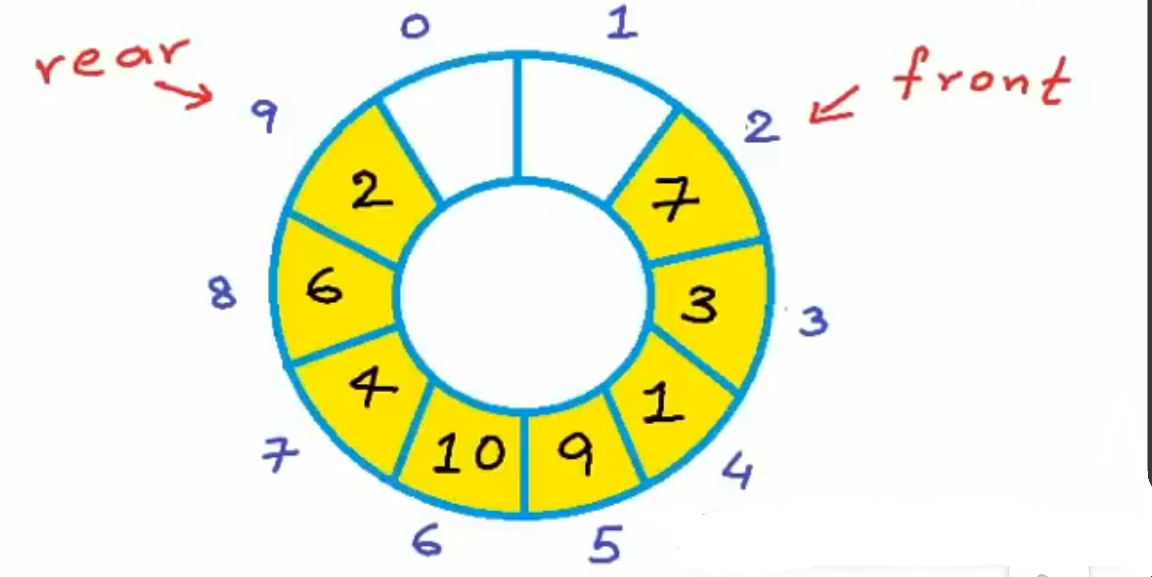
The circular array diagram

When the index is 9, the next index should be 0. So, the index calculating method is changed. If current index is i, the next index should be ( i+1 ) % N. (% means modulo operation, N is the number of the elements. ) And previous index should be (i + N - 1) % N

Therefore, the pseudocode should be modified. The modified part is highlighted.

// for the circular array, the queue can be implemented as follow. (qseudocode)
LinearArrayImplementation(){
	int A[10];
	front <- -1;
	rear <- -1;
	// for an empty queue, the front and the rear are both equal to -1.
}
IsEmpty(){
	if front==-1 && rear == -1
	return true
	else
	return false
}
IsFull(){
	if (rear + 1) % N == front
	return true
	else
	return false
}
Enqueue(){
	if IsFull()
		print "queue is full"
		return
	else if IsEmpty()
		front <- rear<0
	else
		rear <- (rear+1) % N

	A[rear] <- x
}
Dequeue(){
	if IsEmpty()
		return
	else if front==rear
		front <- rear <- -1
	else
		front <- (front + 1) % N
}

However, the array implementation can’t solve the full memory problem. If the memory is full, we choose to reject enqueue or create a new larger array and copy data.

Linked list implementation

If we choose linked list to achieve the queue, we need to set the direction of enqueue and dequeue.

Inserting or removing elements from the head or tail of linked list has different time complexity, but we need enqueue or dequeue in the constant time.

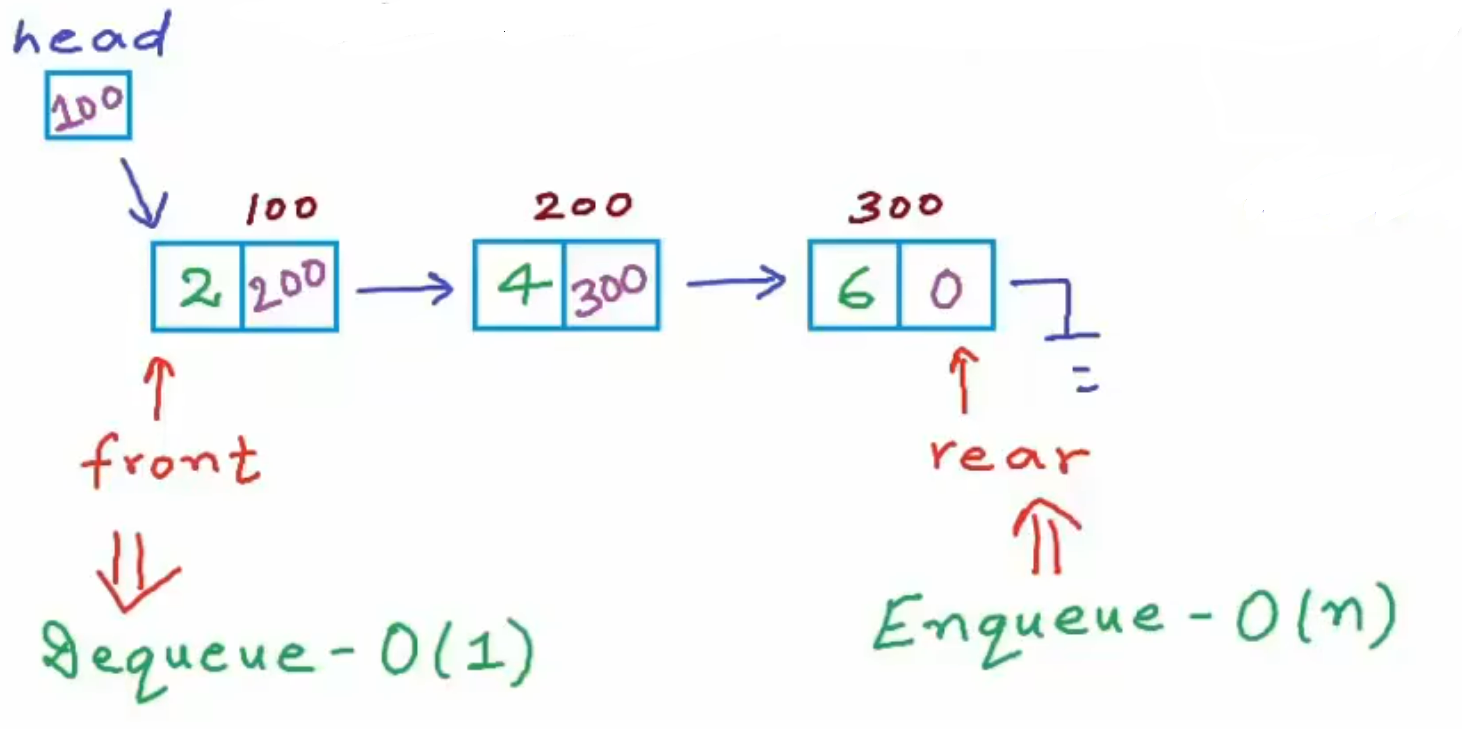
To solve this unbalanced time complexity, we choose to set a new pointer — rear, like the figure below.

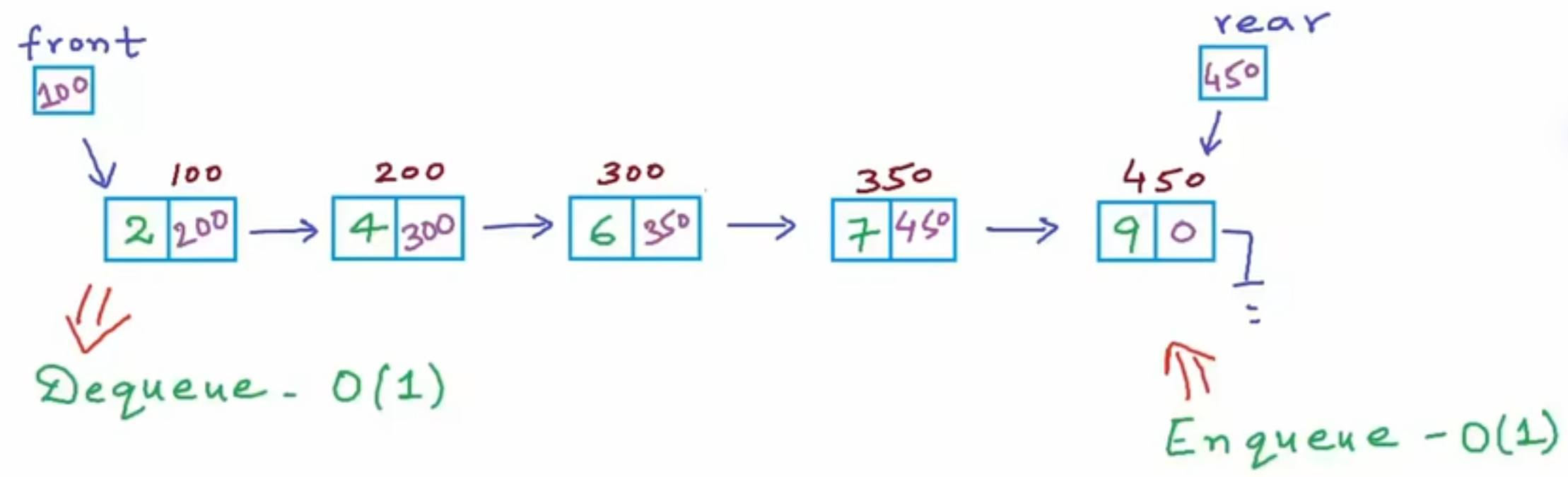
The queue can be implemented by C/C++.

#include<iostream>
using namespace std;

struct Node{
	int data;
	Node* link;
};
Node* front = NULL;
Node* rear = NULL;
bool IsEmpty(){
	if (front == NULL && rear == NULL){
		return true;
	}else{
		return false;
	}
}
void Enqueue(int x){
	Node* temp = new Node();
	temp->data = x;
	temp->link = NULL;
	if (IsEmpty()) {
	front = temp;
	}else {
		Node* temp1 = front;
		while (temp1->link != NULL){
			temp1 = temp1->link;
		}
		temp1->link = temp;
	}
	rear = temp;
}

void Dequeue(){
	Node* temp = front;
	if (IsEmpty()){
		return;
	}else if (front == rear){
		front = NULL;
		rear = NULL;
	}else {
		front = front->link;
		delete temp;
	}

}

void Print(Node* p){
	if (p == NULL){
		cout<<endl;
		return;
	}
	cout<<p->data<<" ";
	Print(p->link);
}

int main(){
	Enqueue(2);
	Enqueue(5);
	Enqueue(6);
	Dequeue();
	Dequeue();
	Dequeue();
	cout<<"List is: ";
	Print(front);

}