🌳 Trees

OYH大约 4 分钟

🌳 Trees

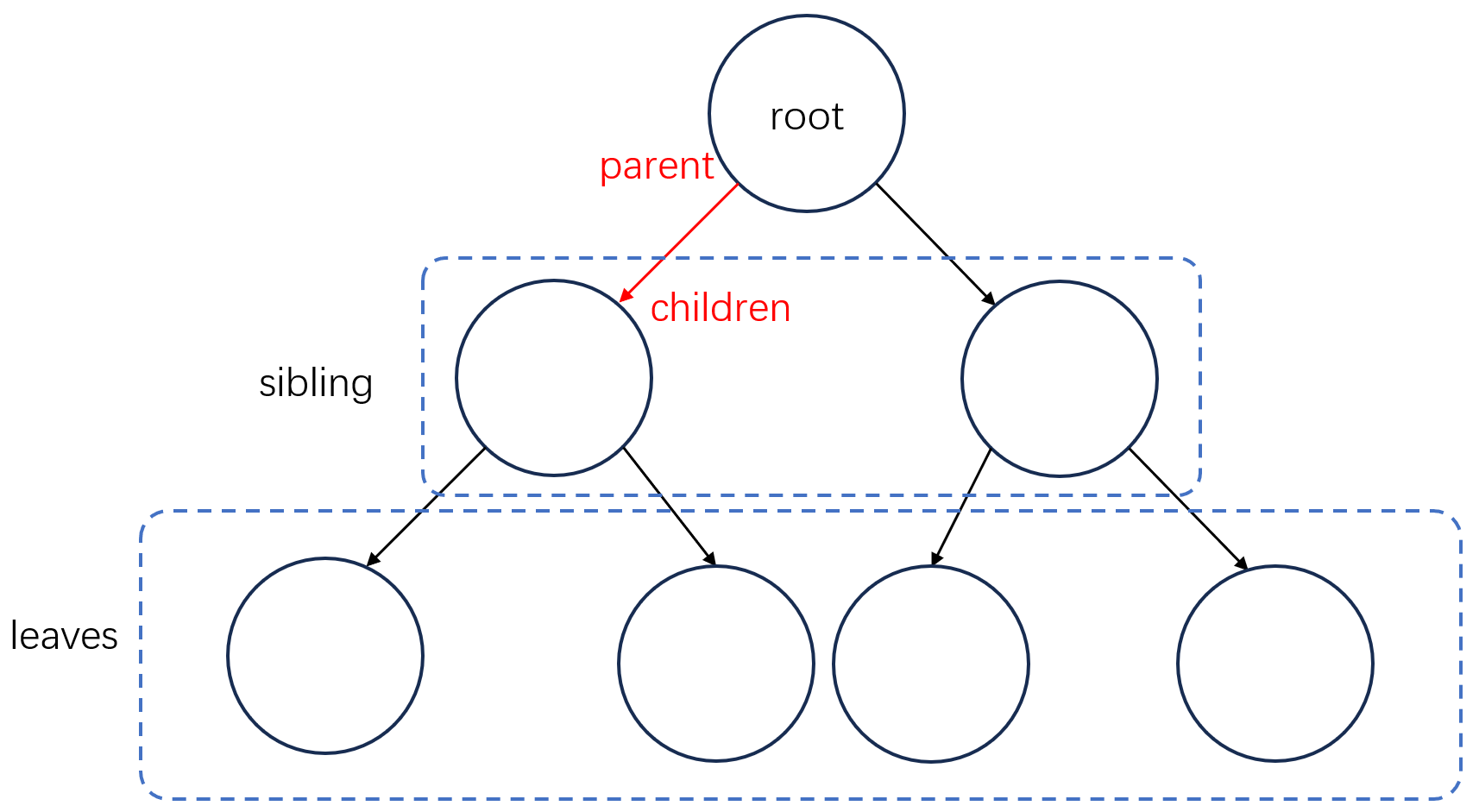
Definition: A tree is a set consisting of several finite nodes with hierarchical relationships.

Features: root, children, parent, sibling, leaves, (ancestor, descendent, cousin)

Tree can be seen recursive data structure.
Tree has N Nodes, and N-1 edges.
Depth of x is defined as the number of edges in path from root to that node.
Hight of x is defined as the number of edges in the longest path from the node to a leaf node.

Logistic View:

Applications:

Storing naturally hierarchical data, eg: file system.
Organizing data for quick search, insertion, deletion, eg: binary search tree.
Trie, eg: dictionary.
Network routing algorithm.

Binary tree

Binary tree is a tree in which each node can have at most 2 children.

Relative conception:

Complete Binary tree: all leaves except possibly the last are completely filled and all nodes are as left as possible.

Most nodes at level i is $2^i$ .

Perfect Binary tree: All nodes should be completely filled.

If the height of the perfect binary tree is $h$ , the max number of binary trees, namely the nodes number of a perfect binary tree, is $2^{h+1} - 1$ , equal to $2^{\text{number of levels}}-1$ . So if we have a perfect binary tree with $n$ nodes, we can calculate the max height of this tree, that is $h=log_2(n+1)-1$ , which is relative to the time complexity of searching. For the complete binary tree, height of the tree is $\left \lfloor log_2(n) \right \rfloor$ (proof omitted). In the binary search tree, when we calculate the cost and complexity of searching, we wanna the height of the tree to be less, that is the tree would be denser, be closer to a complete binary tree. In addition, we let the height of an empty tree to be -1.

Balanced Binary Tree: Difference between the height of left and right subtree for every node is not more than k (mostly 1).

Diff = |h_{left}- h_{right}|

Time complexity difference between several structures with binary search

If you want to know more about binary tree, please look up on Wiki below.

Binary search

	Arrays(unsorted)	Linked List	Arrays(sorted)	Binary Search Tree (Balanced)
Search(x)	O(n)	O(n)	O( $log_2n$ )	O( $log_2n$ )
Insert(x)	O(1)/O(n)	O(1)/O(n)	O(n)	O(l $og_2n$ )
Delete(x)	O(n)	O(n)	O(n)	O( $log_2n$ )

So we introduce the binary search tree, in which we can make each step accomplished in shorter time.

Binary search tree is a binary tree, in which for each node, the value of all the nodes in the left subtree is lesser or equal, and the value of all the nodes in the right subtree is greater.

Implementation in C/C++

#include<iostream>
using namespace std;
struct Node{
	int data;
	Node* left;
	Node* right;
};

Node* getNewNode(int data){
	Node* root = new Node();
	root->data = data;
	root->left = root->right = NULL;
	return root;
}

void Insert(Node** rootPtr, int data){
	if(*rootPtr == NULL){
		*rootPtr = getNewNode(data);
	}else if (data<=(*rootPtr)->data){
		Insert(&((*rootPtr)->left), data);
	}else{
		Insert(&((*rootPtr)->right), data);
	}
}

bool Search(Node* root, int data){
	if (root == NULL){
		return false;
	}else if (root->data == data){
		return true;
	}else if (root->data > data){
		return Search(root->left, data);
	}else{
		return Search(root->right, data);
	}
}
int findMin(Node* root){
	if (root->left == NULL) return root->data;
	else findMin(root->left);
}

int findMax(Node* root){
	if (root->right == NULL) return root->data;
	else findMax(root->right);
}

int findHeight(Node* root){
	if (root == NULL) return -1;
	return max(findHeight(root->left), findHeight(root->right)) + 1;
}

int main(){
	Node* root;
	root = NULL;
	Insert(&root, 25);
	Insert(&root, 20);
	Insert(&root, 10);
	Insert(&root, 15);
	cout<<Search(root, 20);
	cout<<findMin(root);
	cout<<findMax(root);
	cout<<findHeight(root);
}

The above code includes several operations on tree, like insert elements, search elements, find min, find max and return height. In this section, we use recursion to simplify the code. Be careful and notable to that.

Binary Tree Traversal

Tree traversal: the process of visiting each node in the tree exactly once in certain order. It can be classified as the breadth first and the depth first.

Breadth First: level-order In this method, we use a queue to store the address of discovered node. Before we visit or operate the node, we need make its left and right children address enqueue in order. We can easily implement this method in C++, like this, just a loop.
```
void LevelOrder(Node* root){
	if (root == NULL) return;
	queue<Node*> Q;
	Q.push(root);
	while (!Q.empty()){
		Node* current = Q.front();
		cout<<current->data<<endl;
		if(current->left != NULL) Q.push(current->left);
		if(current->right != NULL) Q.push(current->right);
		Q.pop();
	}
}
```
Then, let’s talk about time complexity and space complexity. In this method, visiting a node just need the constant time. Each node just be visited once. So if a binary search tree has n nodes, the time complexity of level order Traversal is $O(n)$ . For space complexity, the usage of the queue is dynamic and doesn’t depend on the number of nodes. The best performance is $O(1)$ , but the worst and average performance is $O(n)$ .

Depth First:

<root><left><right> Preorder (DLR)
<left><root><right> Inorder (LDR)
<left><right><root> Postorder (LRD) By recursion, this can be achieved easily.

void LDROrder(Node* root){
	if (root==NULL) return;
	LDROrder(root->left);
	cout<<root->data<<" ";
	LDROrder(root->right);
}

void DLROrder(Node* root){
	if (root==NULL) return;
	cout<<root->data<<" ";
	LDROrder(root->left);
	LDROrder(root->right);
}

void LRDOrder(Node* root){
	if (root==NULL) return;
	LDROrder(root->left);
	LDROrder(root->right);
	cout<<root->data<<" ";
}

Is it the binary search tree?

We use recursion to tell whether a tree is a binary search tree or not.

bool IsSubtreeLesser(Node* root, int value){
	if (root == NULL) return true;
	if (root->data <= value
		&& IsSubtreeLesser(root->left, value)
		&& IsSubtreeLesser(root->right, value)
	) return true;
	else return false;
}

bool IsSubtreeGreater(Node* root, int value){
	if (root == NULL) return true;
	if (root->data > value
		&& IsSubtreeGreater(root->left, value)
		&& IsSubtreeGreater(root->right, value)
	) return true;
	else return false;
}

bool IsBinarySearchTree(Node* root){
	if (root == NULL) return true;
	if(
		IsSubtreeLesser(root->left, root->data)
		&& IsSubtreeGreater(root->right, root->data)
		&& IsBinarySearchTree(root->left)
		&& IsBinarySearchTree(root->right)
	) return true;
	else return false;
}

How to delete a element in a binary search tree?

It’s very complex to delete a element in a binary search tree. After deletion, we need to maintain the tree still is the binary search tree.

We can divided this problem as three cases: 1) if the node doesn’t has child node. 2) if the node has only one child node. 3) if the node has two child nodes.

For the first case, we should easily delete the node and free the memory. That will be okay.

For the second case, we should make its parent node’s pointer point to its child node.

For the third case, we should wipe off the data of this node, and find the min value in its right subtree. Then, copy the value in targeted node and delete duplicate from right-subtree.

Node* Delete(Node* root, int data){
	if (root==NULL) return root;
	else if (data <= root->data) root->left = Delete(root->left, data);
	else if (data >= root->data) root->right = Delete(root->right, data);
	else {
		if (root->left ==NULL && root->right == NULL){
			delete root;
			root = NULL;
		}
		else if (root->left == NULL){
			Node* temp = root;
			root = root->right;
			delete temp;
		}
		else if (root->right == NULL){
			Node* temp = root;
			root = root->left;
			delete temp;
		}
		else{
			int temp = findMin(root->right);
			root->data = temp;
			root->right = Delete(root->right, temp);
		}
		return root;
	}
}